PID

 PID 

A proportional-integral-derivative controller (PID controller) is a common feedback loop component in  ndustrial control systems. The controller takes a measured value from a process or other apparatus and compares it with a reference setpoint value. The difference (or "error" signal) is then used to adjust some input to the process in order to bring the process' measured value back to its desired setpoint. Unlike simpler controllers, the PID can adjust process outputs based on the history and rate of change of the error signal, which gives more accurate and stable control. PID controllers do not require advanced mathematics to design and can be easily adjusted (or "tuned") to the desired application, unlike more complicated control algorithms based on optimal control theory.


Introduction of PID Control
1. PID Operation Principles

Most of controls extensively used in the process control of modern industries have

PID(proportional Integral Derivative) structure, whose structure is simple and easy to

control.

PID control means outputting proper operation values (output values, CV) to the

object of control by calculating the differences of PVs and SVs and PVs by

proportional (P), Integral (I) and Derivative (D) operation to the measured value of

control object (PV) and user's set value (SV).

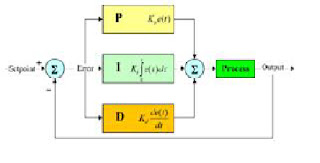
The following is a figure for understanding the concept of PID operation.

PID block diagram 

2. Proportional Operation (P Operation)

This means the operation to eliminate the differences between the set values (SV) by

users and present values (PV).

This operation obtains control values proportionate to the differences, which can be

indicated as the following equation.

CV = Kp • E

Kp is a proportional integer (gain) to fix if the proportional operation can be strong or

weak. Errors (E) is directly multiplied to Kp, so the bigger Kp becomes, the bigger

Error values does. As shown the figure below, it is found that high Kp value makes CV

high to equal E, that is, strong proportional operation, but low Kp does CV low.

Generally, if Kp is high (proportional operation is strong), PV quickly approaches SV.

However, if it is too high, it has a bad impact on control stability such as too big a

vibration.

Also if Kp is too small, vibration does not generate, but the speed of Pv approaching

SV slows down, remaining deviation (error in normal state, OFFSET) may occur.

The following figure is a concept map of PV by proportional operation.

3. Integral Operation (I Operation)
Integral operation continuously compensates for the differences occurring between
user's set values (SV) and present values (PV).
Adjusting integral time (,kt) of integral operation can make strong or weak operation
as above. That is, the longer the integral time (,kt), the shorter the changed amount of
CV becomes. Thus, the time of PV approaching SV becomes long, if integral time is
short, the added and reduced amount to CV becomes large, so PV approaches SV in
a short time.
The following figure is the concept map of integral map when Errors occur.

As the above figure, if integral time is too short, PV quickly approaches SV, but PV
can diverge, if it is too long, PV slowly does SV.


4. Derivative Operation (D Operation)
If user changes set values (SV) or present values change due to external influences,
the differences of set values (SV) and present values (PV) also change. Derivative
operation restrict this operation. The following formula is the numerical expression by
derivative operation.

As the above formula, the longer the integral time is, the stronger the restricting
operation of change rate of E, while, the shorter the time, the weaker the operation.
The following figure is the concept map of derivative operation.

Derivative operation is not used solely, but in P operation or P-I operation or
combined P-D, P-I-D.
Generally the control using derivative operation makes the speed of PV approaching
SV rapid, and has effects of radical change or external change of PV.


5. PID Calculations
The following table is the description to calculation numerical formula, normal/reverse
operation and output type of controlled value. The constant used in ISA algorithm and
Independent gain algorithm is differently expressed, but the meaning is the same as
that below.

6. Independent Gain equation

w here:

CV = output
K p = proportional g ain constan t (unitle ss)
K i = integral g ain constant (1 / sec)
K d = derivative g ain constant (1 / sec)
d t = time b etween samples (minutes)
B ias = feed forward o r output b ias
E = error equal to (PV - SP) o r (SP - PV)
PV = process v ariable
E (n - 1) = error from last sample
PV(n - 1) = process v ariable from last sample

7. ISA equation

where:

CV = output
K c = controller gain constant (unitless)
T i = reset gain constant (minutes per repeat)
T d = rate gain constant (minutes)
dt = time between samples (minutes)
Bias = feed forward o r output bias
E = error equal to (PV - SP) o r (SP - PV)
PV = process variable
E(n - 1) = error from last sample
PV(n - 1) = process variable from last sample

8. Normal/Reverse Operation

Normal operation is the type of increasing controlled values to draw up present values
(PV), reverse operation is that of increasing CVs to draw down PVs. The control type
by normal and reverse operation is as follows.

http://www.mediafire.com/?231n8dutts3d6z0
DOWNLOAD PIDMON PID guide pdf